Research

My research lives in the intersection of discrete mathematics and theoretical computer science, with a focus on colouring, homomorphisms, and structural properties of directed, signed, and edge-coloured graphs. Much of my work is concerned with understanding how classical notions from graph theory, such as chromatic number, behave when extended to settings where edges carry additional structure, such as directions, signs, or colours.

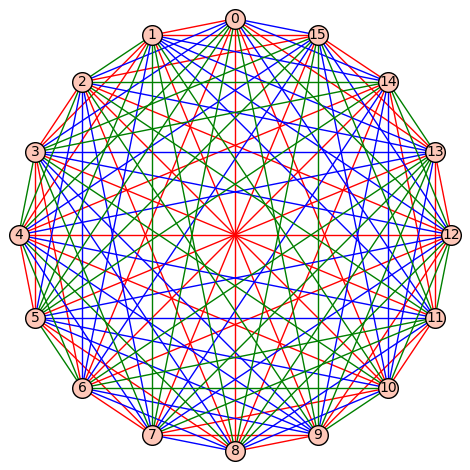
I am also interested in switching operations and symmetry in graphs with arcs and/or edge colours. The image below gives a largest example of a 3-edge-coloured graph that cannot be switched (with respect to elements of \(C_3\)) to contain a monochromatic \(K_4\). Interestingly, this graph was previously known in the literature as one of two largest examples of 3-edge-coloured graphs that contains no monochromatic \(K_3\). That the graph cannot be switched to contain a monochromatic \(K_4\) was shown by B. Fok, an undergraduate student working with me on a semester-long research project in 2025.

A significant part of my research involves collaboration with students. My research program has open lines of enquiry suitable for students at all levels. In particular, I am always looking for undergraduate students who are interested in research in discrete mathematics and/or theoretical computer science.

A full list of my publications is available here